Consciousness, Energy, and Life: An Uncommon Perspective
Harmonizing Science, Philosophy, and Meaning in a Unified Metatheory that Explores Macro-Interconnections and Our Place in the Cosmos.
Update (Jan 8, 2025): Although I am still in the process of writing the FMHR paper, you can already download a version of this post in a more formal, paper-like format if you wish. The PDF has also been optimized to be AI-friendly, for smoother interactions with conversational AI platforms. The Discussion section has been intentionally omitted from this excerpt to minimize the potential for confirmation or framing biases when engaging with AI.
Disclaimer 3
Hello welcome to the final installment of the three-part series titled: The Nature of Light & Dark Energy—Exploring the Interplay of Physics, Consciousness, and Hidden Dimensions. In this concluding chapter, we delve deeper into the Hyperdimensional Resonance Theory (HRT), but not exactly building upon the foundational ideas and thought experiments introduced in part one and two.
This series attempts to forge a novel perspective on the interconnectedness of life, the universe, and our perception of reality. As an integrative theorist in this series, my aim has been to stimulate thought, encourage intellectual risks, and push the boundaries of scientific imagination. I approach this not as an expert in cosmology, quantum mechanics or modern physics, but as someone driven by curiosity and a desire to synthesize complex multidisciplinary conjectures into a cohesive narrative.
Unlike part one and two controversial arguments over spacetime physics, in this final installment I blend the insights from renowned scholars and intellectuals to propose a multidisciplinary depiction of seemly disparate concepts to propose a new hypothesis, laying the grounds for HRT to be branded as a metatheory and seen as a proposition that attempts to bridge some gaps between science and what some would describe as perennial philosophy, using contemporary and classic theories, modern narratives and scientifically grounded conjectures to “soft fill” the societal void left by declining traditional theological values and frameworks, and the modern societal crisis for meaning, lacuna overly explored by pure materialism and shallow religious principles.
As a metatheory, HRT attempts to acknowledge humanity’s need for deeper meaning and connection. By grounding its foundations in physics and cosmology, exploring the philosophy of science and making use of these as backdrop to elaborate over the interconnectedness of life, the universe and experiences that transcend siloed and perhaps even hollow ontologies, HRT attempts to stimulate coherent curiosity and wonder, not to be a pragmatic nor dogmatic “truth” of any type.
Ultimately, HRT’s blend of scientific rigor and philosophical speculation is a thought experiment, and I hope that it serves as a catalyst for fresh ideas, for a broader lateral thinking in science in this era of hyper-specialization, perhaps even as a foundation for a more beautiful depiction of reality, and a step toward uniting science with a more meaninful narrative of all there is. Thank you for reading this series.
Abstract
This post builds on Theories of Consciousness and Quantum Mechanics to introduce the Field-Mediated Holographic Resonance (FMHR) hypothesis. It proposes a radical new mechanism for inter-brain information transfer via the quantum vacuum field. Through a sophisticated Hamiltonian formalism, FMHR demonstrates how neural activity patterns may be encoded holographically in vacuum field modes, enabling autonomous information transfer between random neural systems. The hypothesis provides new perspectives over long-standing questions about quantum effects in biological systems with rigorous mathematical treatment, proposing new directions for understanding non-local neural information transfer in biological neural networks.
On the Limitations of Dreams
While dreaming, humans don’t often experience much beyond personhood: We do not dream of being a bee, being air, being the moon, or yet another random interspecies experience. We do not dream of being a wolf belonging to a pack, nor being aliens in their own home planet, although we can dream interacting with such things from our own subjective construct of ourselves: we dream of reacting over some bees, seeing the moon, being with other people, animals and aliens, not experiencing their point of view of reality. The “self” is not just a psychological construct, it is a deeply embodied state of self-perception, very deterministic in not transcending ones’ own sensory boundaries (please let me know if you ever dreamt of being gasoline or a house plant).
While it ain’t wise to claim biological determinism entirely governs dreams, given brain structure and genetic predispositions I humbly believe biological determinants would carry more foundational weight than other factors that compose a dream. Given this assumption, I think it may be possible to broadly capture which other parts of life compose a dream experience, with a formula like:
Where:
D = Dream content and experience;
βB = Emphasizes the strong influence of biological determinants;
I = Imagination (mental skills for creativity, abstraction, and novel scenarios);
P = Psychological factors (cognitive processing, mental state, subconscious desires, emotional processing);
S = Sensorimotor experiences (input from the body’s senses in waking life, e.g., vision, hearing, touch, proprioception, and kinesthetic awareness);
C = Cultural influences (cultural narratives, educational background, languages learned, myths);
H = Social and historical context (social dynamics, historical background, societal norms, and individual experiences).
Where internal factors ϕ(I,P,S) and external factors γ(C,H) are grouped together and ψ(I,P,C,H) represents the complex interplay between all these factors. Surely a simplification, this dream equation offers an initial framework to see how biological factors (B) might interplay with other factors (C,H,I,P,S), offering a more holistic model for describing dreams than strictly biology or psychology-driven depictions.
I do not think I’d be misinforming you in saying that dreams are more often than not centered around “me” experiences because apparently they are part of the brains’ memory consolidation, emotional processing, and other reinforcing mechanisms tied to B+CH+IPS dynamics and the “me-centric” continuity expression and focus, which would perhaps explain why we don’t often dream of being the mayor of some unknown city in the Philippines, learning a new skill unrelated to our experiences or having unusual behaviors such as speak in languages we were never primed to understand. But the way dreams are composed by their dreamers reflect one particularly interesting characteristic of ourselves: we do not know what we do not know; or better phrased by Galileo more than 400 years ago:
"Philosophy is written in this grand book, the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and read the letters in which it is composed". From: The Assayer.
Dreams, standing at the full power of the most amazingly creative engine known to man, cannot independently dream of things we can imagine while awake, for they cannot offer us what we don’t understand. But even wide awake, it seems evident that we cannot imagine our way in learning to swim or becoming lawyers, for imagination, while more expressive than dreams themselves, also cannot imagine learning a never seen craft in its full form and details.
In describing the unfolding of our awareness, the Swiss philosopher Jean Gebser defined five main structures of consciousness, starting with a more sensory experience towards the gradual transcendence of limitations of previous structures, then evident by one’s interconnectedness with space and time, a type of path towards what he called an “aperspectival consciousness” that allows freedom of perspective to be spontaneously experienced. For Gebser, we can only experience the abstract—what lies beyond mental-rational consciousness—after we understand our own awareness.
So here I will leave you with a thought exercise: If humans could read thoughts, would a person who never experienced skydiving understand the thoughts of a person who did?
This question should make you pause and consider how “reading thoughts” would work in real life: would you understand the thoughts, the feelings or both? For as dreams tell us—brains are not very good in translating what it never experienced.
The Cosmic and the Consciousness
In 1901, psychiatrist Richard Bucke first published “Cosmic Consciousness: A study in the evolution of the human mind”, where Bucke states that beyond mere simple consciousness—common to animals and humans—and self-consciousness—exclusive to mankind, governing reason and imagination—there also exists a third “flavor” of consciousness, one that transcends death and matter towards the “top layer of the world of self consciousness mental stratum”. Bucke describes this state as a type of illumination, a state of awakening common to all those who experience the effects of this so called “cosmic consciousness”, going in detail on the commonalities of this state as experienced/reported by Jesus, Dante, Spinoza, Gautama, Bacon, Pascal, towards an interesting conclusion: such phenomenon is increasingly more universal, more frequent. But what is this state of oneness if not a mystical experience? Even more intriguing: Why we describe these experiences using such common narratives, no matter the time, the race, the language or the objective exposure/causality?
Jung creatively termed this phenomenon “synchronicity” in an attempt to describe how meaning can emerge from acausal systems as a quasi esoteric or religious connection. Jung also rejected the idea of tabula rasa, proposing instead that all humans have innate behavioral patterns or archetypes, that are common to a type of world soul or what Jung defined as collective unconsciousness, a repository of mental concepts that then explains why similar explanations occur in describing mystical experiences, something akin to how the concept of monopsychism describes that humans share the same “mind” or that the mind is a fundamental feature of reality.
Nowadays, we can imagine the internet to be the most popular realization of the idea of some collective “oneness”, a digital noosphere—a planetary layer of reason that transcends our geosphere and biosphere—our contemporary attempt to recreate what previous generations described only in mystical terms. But the creation of the cyberspace did not addressed the serendipity experienced across the globe. Sure, it has become yet another medium for coincidences, for the search for meaning in the next post, the next story, the next podcast, but after years of existence, the internet further isolated us from one another and from experiences that are real, but most of all, no technology has yet answered why humans across the world still experience thoughts and feelings that cannot be explained by science. From a more mundane depiction than of those of a mystical nature, why we all do experience things like:
A thought, an idea, that some time after naturally emerging in your mind, appears in your phone, in your surroundings, or in a conversation some time later;
We think or dream of someone, something, and it “manifests” to us;
A feeling of unexplained joy or sadness that simply “arrives”;
Dissociation, awe, déjà vu, or a type of intuitive insight or solution for a specific situation that comes out of thin air;
Mental illnesses (and hollow mysticism) aside, these experiences give credence to the concept of an universal mind, an omnipresent mental unity that contains all knowledge and is experienced at random (an important distinction is that access to such unity is not available at will). So how does modern science address such ancient experiences? Spoiler: it kinda doesn’t.
Classic and Quantum Mechanics of the Mind
Consciousness is something that unlike bodily dynamics, cannot be described by its physical motion or properties of its particles. The standard model cannot describe consciousness as one simple flow of neurons or mere biochemical properties, only infer over where some reactions take place, such as pinpointing the Broca’s and Wernicke’s brain regions as locations often linked to language and speech production, or the brainstem as being mainly responsible for breathing and many other motor functions (there’s even those who believe the brainstem to also host consciousness itself). In other words, we can’t really pinpoint [yet] what self or qualia is.
From a philosophical perspective, physicalism should rule consciousness (as in, “we think, therefore we are” is only possible because the brain is there) a position further explored by the more skeptical epiphenomenalism (which states both the act of raising my hand and the decision itself are then byproducts of physical processes), and both narratives describe consciousness from a deterministic/causal perspective. And while physicalism itself is indeed the frame of reference for most major theories of consciousness, particularly in understanding the nature or role of self and cognition, the idea that consciousness is not just a passive byproduct, but instead an active and influential force for what brains do is largely a consensus between these theories, rejecting epiphenomenalist foundations from an empirical (non-deductive) standpoint. But while it is certainly reasonable that the standard model should be the current background to describe key physical aspects of such dynamics, how the rules of quantum mechanics fit in this domain?
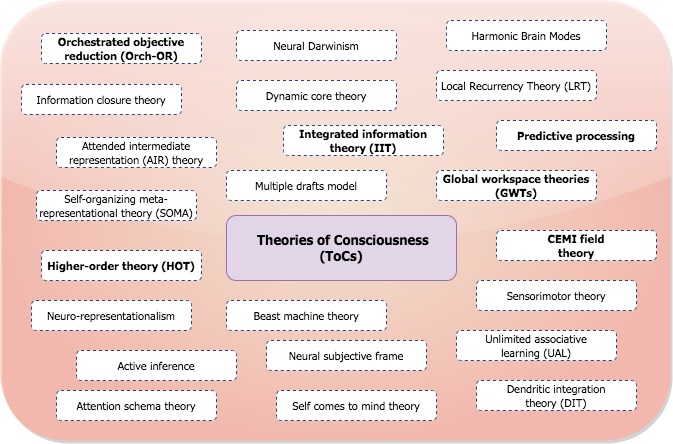
Similar to mainstream theories of consciousness (ToCs), there are also quantum consciousness theories that investigate (or postulate over) macro neurophysiological processes via quantum physics and its laws as an attempt to explain effects and dynamics that may arise from interactions between classic and quantum mechanics. For brevity’s sake, I have asked Mistral AI to generate a list of some of these theories, along with a brief description of each and its key concept. Some of these are presented in Table 1 below, listing those I personally find most intriguing.
Beyond the more obvious overlaps in depth and scope of these theories, the consensus among them is reasonable: quantum mechanics may serve as a bridge, elaborating over how quantum phenomena can impact classical neurobiological processes. And while some models do not directly assume quantum processes in the human brain, making instead use of quantum theory to explain them, others as Penrose and Stapp see the brain quantum properties having a significant role in both consciousness and the brain inner workings. However, I pose the question: Is it possible to extend these theories—not by building on them incrementally or merging its ideas, but by providing them with a new foundational background?
What if we could instead utilize quantum mechanics to formalize a new hypothesis for a more elementary form of quantum physics dynamic? Could then the ideas of Bohm, Pitkänen, Pribram, and Aerts have new grounds to explore? Is it possible to apply the framework of scientific skepticism to move beyond siloed interpretations, and forge more novel, inclusive narrative for what brains may be capable of?
A Field-Mediated Holographic Resonance Hypothesis

The Field-Mediated Holographic Resonance Hypothesis (FMHR) builds upon a multidisciplinary integration of several established frameworks, including Quantum Field theory in curved spacetime, Pribram’s Holonomic Brain theory, neural quantum coherence states, Biophotonic emission patterns, nonlinear dynamics and Information Theory in biological systems. The conceptual refinement of this proposal is that it does not attempt to explain consciousness nor compete with other theories of consciousness, instead, it postulates a mechanistic process for non-local information sharing using established physics to depict a scientific framework for a phenomenon that many individuals intuitively sense exist, but which have often been avoided or left unexamined within mainstream scientific discourse.
Introduction and Theoretical Framework
Unlike theories that attempt to directly explain consciousness itself or posit a causal influence of quantum mechanics on its processes, the Field-Mediated Holographic Resonance Hypothesis (FMHR) proposes a distinct dynamic: neural systems maintain a continuous flow of quantum coherence states that correspond to ongoing classical brain activity, spanning from atomic to macroscopic scales (e.g., synaptic events). Critically, the hypothesis posits that fragments of these quantum states can be autonomously and spontaneously imprinted onto the fabric of spacetime, in the zero-point field (ZPF). This dynamic is mathematically characterized in Hamiltonian terms in the next section, with Ĥint representing the interaction between neural and vacuum field oscillators.
Importantly, quantum states within FMHR are hypothesized to arise from neural coherence patterns mediated by subcellular structures such as microtubules, dendritic networks, or ion channels, alone or combined. Given the continuous nature of the brain neural activity, these structures potentially maintain and renew quantum coherence over biologically relevant timescales, enabling continuous or semi-sporadic interactions with the ZPF. This quantum information is represented here using density matrices, where they encapsulate the coherence and entanglement properties of the imprinted neural information, enabling its probabilistic retrieval and the quantization of statistical properties of quantum states.
Analogous to a photograph—a two-dimensional snapshot of a four-dimensional spacetime event, capturing a specific moment in time and the spatial arrangement of matter and photons—a brain’s quantum coherence “snapshot” reflects a partial, contextual, and transient state within the brain’s complex physiological and structural dynamics. This “4D quantum coherence state photography”* captures a transversal cross-section of neural processes at a given moment, representing a quantum-level counterpart state to the ongoing chain of biochemical and bioelectrical activity that ultimately give rise to conscious thought. *4D here stands for spacetime.
As illustrated in Figure 1 by a downward-pointing diagonal arrow with numerous degrees of freedom, the capture reflects a singular multidimensional temporal event (dynamic oscillations) that can span across multiple levels of organization (from the quantum field level to macro-scale processes like consciousness) and across different types of processes (events, physiological). Crucially, the information volume and specific data reflected by such a state are not the primary focus of this article, which aims to postulate the mechanics and probabilities of this capture event and suggest dynamic reactions, not its particular characteristics.

The capture mechanics is proposed to take place via interaction between neural coherence states and the quantum vacuum field, resulting in the probabilistic imprinting of fragments of the brain’s quantum coherence states onto spacetime. Moreover, this imprinting arises from a dynamic coupling between the oscillating patterns of neural activity and quantum vacuum fluctuations, resulting in a subtle modulation of the field’s state. These modulations encode partial and contextual “snapshots” of ongoing neural processes, encompassing bioelectrical triggers, biochemical chains, synaptic events, emergent brain activity, and even possible “prompts” of thought cascades, here termed proto-thoughts. The fidelity of these imprints varies based on the dynamic nature of both neural activity and quantum vacuum fluctuations, reflecting the probabilistic and partial nature of the capture.
💡Proto-thought: In the context of the FMHR, a proto-thought refers to a quantum-level counterpart stimuli of probabilistic synaptic correlations—the complex and interconnected network of neural connections that precede the constitution of a fully formed idea. For FMHR, creativity is seen to emerge from the fusion of diverse ontologies, experiences, and influences. Akin to a strange attractor, a proto-thought can perturb the system, nudging it toward new basins of attraction, with a potential to also act as trigger for ranges of associative pathways. Unlike structured, rational, or accessible thoughts, a proto-thought is then seen as a signaling fragment that can “join” complex cascades of neural activity, potentially influencing neural decoding processes and leading to uncommon sparks of creativity or conceptualizations. In other times, a proto-thought may be composed of nudges of implicit learning triggers, or even the collective representation of concept cells content. As an analogy, one originally made by Bohm, the proto-thought can be seen as a TV signal that is too weak to produce an image on the screen, but a real signal nonetheless. The interplay of deterministic evolution, stochastic fluctuations, and decay is mathematically described in section’s 2 by the quantum state evolution equation.
FMHR further proposes that the information encoded within the quantum vacuum can be autonomously and probabilistically “read” or “decoded” by other similar neural systems. Drawing inspiration from Pribram’s holonomic brain theory—which suggests that information is distributed throughout the dendritic arbor in a holographic-like manner—FMHR posits a viable mechanism by which the captured quantum information within the vacuum can interact with the dendritic arbor of a receiving brain, potentially triggering resonant oscillations or influencing existing coherence patterns within receiving neural networks.
This holographic encoding process within FMHR is mathematically analogous to the Fourier transform, where phase and amplitude components of neural coherence states are modulated into quantum wavefunctions within the ZPF. This encoding allows for distributed information storage akin to holographic principles, where each fragment contains information about the whole neural state. Moreover, neural coherence patterns information is thought to be encoded in the quantum state’s amplitude and phase components, akin to how classical signals are represented in the frequency domain, enabling the ZPF to act as a probabilistic repository.
Also probabilistic in nature, the reception of this information is considered to be influenced by factors such as the receiving brain’s current state and the status of the vacuum field modulation. This probabilistic reception model explains why not every brain necessarily “picks up” every imprinted fragment available around us, or that if they do, particular brains may lack the required assets to stimulate its processing. This also accounts for the partial nature of the capture, as only certain aspects of the ZPF perturbation may resonate with a given receiving brain.
Formulations
The following equations provide a mathematical framework describing how the ever-present quantum vacuum field around all of us continuously functions as an information-encoding medium for brain coherence states. Through quantum field interactions, neural activity creates probabilistic perturbations in the vacuum field that encode information in a distributed, holographic-like manner. These perturbations represent partial quantum states of neural activity, continuously evolving as the brain’s coherence states change. The framework demonstrates how this encoded information remains accessible to other neural systems through autonomous and spontaneous quantum field interactions, independent of conscious awareness or evident biological signatures. The mathematical formalism that follows establishes the fundamental dynamics and information transfer processes that make this phenomenon theoretically viable.
🖲 1 - Quantum Field Equations
The interaction between neural activity and the quantum vacuum field is described by the following Hamiltonian:
The neural Hamiltonian (Ĥneural) models the brain’s quantum coherent states as an ensemble of quantum harmonic oscillators. The first term, Σiℏωi â†i âi, represents the baseline energy spectrum of neural oscillations, where ωi is defines the natural frequency of the i-th neural mode, with â†i and âi being the quantum operators that create and annihilate these oscillatory states respectively. These modes correspond to various collective neural oscillations, potentially mapping to observed brainwave patterns across different frequency bands (alpha, beta, gamma, etc.). The second term, Σi ℏγi(t, T) â†i âi, introduces a crucial modulation function γi(t, T) that depends on both time and temperature. This term captures the dynamic nature of neural coherence under thermal conditions, where T represents the physiological temperature effects on quantum coherence, and the t time dependence reflects the system’s ability to maintain coherent states despite thermal fluctuations. The γi(t, T) function effectively describes how neural systems might sustain quantum coherence through active biological mechanisms that counteract thermal decoherence.
The vacuum Hamiltonian (Ĥvacuum) represents the quantum vacuum field as a collection of quantum harmonic oscillators, each corresponding to a distinct field mode k. The first term, Σk ℏωk b†k bk, describes the fundamental energy structure of the vacuum field, where ωk represents the characteristic frequency of each mode k, with b†k and bk serving as the creation and annihilation operators respectively. This term characterizes the baseline zero-point energy spectrum of the quantum vacuum. The second term, Σk ℏεk(t, T) b†k bk, introduces a dynamic modulation function εk(t, T) that captures the vacuum field’s temporal and thermal dependence. The time dependence reflects the natural quantum fluctuations of the vacuum, while the temperature dependence T accounts for thermal effects that can modify these fluctuations. Importantly, εk(t, T) represents the vacuum’s inherent dynamics rather than any external influences—it describes how the vacuum modes naturally evolve and fluctuate in time under thermal conditions. These modulations provide the background “canvas” upon which neural-vacuum interactions can potentially happen, though the actual interaction dynamics are reserved for the interaction Hamiltonian.
The interaction Hamiltonian (Ĥint) represents the core mechanism of neural-vacuum field coupling, describing how quantum coherent states in neural systems can create and interact with perturbations in the quantum vacuum. This interaction enables the probabilistic encoding and retrieval of neural information patterns through quantum field modulations.
The interaction is structured through several sophisticated coupling mechanisms:
1. Amplitude Modulation Term - The term [A0 + Σn αn(t) Fn(ρ(x)) + ξ(t)] represents a dynamic coupling amplitude with three key components:
A0: Baseline coupling constant defining the fundamental interaction strength;
Σn αn(t) Fn(ρ(x)): A nonlinear coupling term that maps neural density patterns to field interactions;
ξ(t): Stochastic fluctuations that introduce quantum uncertainty into the coupling.
2. Spatial Encoding of Neural Activity - Fn(ρ(x)) = ∫ d3x ρ(x) Kn(x-x') ρ(x') performs a crucial role:
Integrates neural density patterns across three-dimensional space;
Kernel functions Kn(x-x') define how spatial correlations in neural activity influence field coupling;
Creates a holographic-like encoding by transforming local neural patterns into distributed field perturbations.
3. Mode Coupling Matrix - [ḡik(ωk,t) + δgik(t)] describes the selective coupling between neural and vacuum modes:
ḡik(ωk,t): Frequency-dependent coupling strength between neural mode i and vacuum mode k;
δgik(t): Time-dependent fluctuations in coupling strength;
Together they enable resonant interactions between specific neural frequencies and vacuum modes.
4. Phase and Temporal Modulation
eiφ(t): Phase modulation term affecting interference patterns in the quantum field;
ε(t): Overall temporal envelope controlling interaction strength;
â†i bk + H.c.: Quantum operators mediating energy and information exchange (H.c. denotes the Hermitian conjugate, which ensures the Hamiltonian is a physical observable).
The complete interaction enables three key processes:
Encoding: Neural density patterns create structured perturbations in the vacuum field;
Storage: These perturbations persist as quantum field configurations;
Retrieval: Other neural systems can probabilistically couple to these field patterns.
This sophisticated interaction structure allows for:
Nonlocal information encoding through spatial integration;
Frequency-selective coupling through mode matching;
Temporal evolution of field-neural interactions;
Probabilistic information transfer through quantum field fluctuations.
🖲 2 - Quantum Coherence Evolution
The quantum coherence state evolution of the neural-vacuum system follows a stochastic Schrödinger-like equation that captures both the deterministic dynamics and probabilistic aspects of the field-mediated information transfer:
This equation describes three fundamental processes:
1. Coherent Evolution - The term (-iĤ/ħ)|ψ(t)⟩dt governs the unitary evolution under the total Hamiltonian Ĥ, representing the coherent dynamics of neural-vacuum coupling. This describes how neural coherence states evolve while interacting with the vacuum field, enabling the encoding of neural patterns into field perturbations.
2. Baseline Decoherence - The term (-Γ0/2)|ψ(t)⟩dt introduces a constant decoherence rate through the operator Γ0, representing the system’s inherent tendency to lose quantum coherence due to environmental coupling. This term is crucial as it sets the characteristic timescale over which neural quantum states can maintain their coherence and effectively interact with the vacuum field.
3. Stochastic Fluctuations - The term -(1/2)δΓ(t)|ψ(t)⟩dW(t) introduces time-dependent fluctuations in the decoherence process through:
δΓ(t): A time-dependent operator capturing variations in decoherence strength;
dW(t): A Wiener process introducing controlled randomness;
This stochastic component is essential for:
Modeling the probabilistic nature of neural-vacuum interactions;
Accounting for thermal and environmental fluctuations;
Enabling the emergence of stable information patterns despite noise.
The combined effect of these terms creates a delicate balance between:
Information encoding through coherent evolution;
Natural degradation through baseline decoherence;
Dynamic fluctuations that can either enhance or suppress coherence.
This evolution equation thus provides the mathematical framework for understanding how neural quantum states can maintain sufficient coherence to interact with the vacuum field while still being subject to realistic biological conditions and environmental influences.
🖲 3 - Vacuum Field Perturbation
The vacuum field perturbation pattern Φ(x,t), fundamental to the FMHR mechanism, is characterized by a two-point correlation function that describes how neural-induced perturbations create structured patterns in the quantum vacuum:
This correlation function reveals several key aspects of the field-mediated information encoding:
1. Spatiotemporal Structure
(x,t) and (x′,t′) represent distinct points in spacetime;
Their correlation captures how field perturbations are distributed across space and persist in time;
This distributed nature enables holographic-like information encoding.
2. Mode Decomposition
The integral over k decomposes the field into its constituent modes;
fk(x) represents the spatial structure of each mode;
e±iωkt captures the temporal evolution of the modes;
Together they describe how neural information is encoded across different field frequencies.
3. Quantum Correlations
bk and b†k (annihilation and creation operators) mediate quantum transitions;
Their action creates coherent patterns of field excitations;
These patterns represent quantum correlations that can extend over significant distances and time intervals.
4. Correlation Function C(x,x′;t,t′)
This crucial term:
Encodes the spatial and temporal memory of neural interactions;
Reflects how neural activity patterns become imprinted in the vacuum;
Contains the history of field-neural coupling events;
Determines the stability and accessibility of stored information;
The correlation function serves multiple roles in FMHR:
Information Storage: Shows how neural patterns become encoded in field correlations;
Pattern Stability: Reveals how encoded information persists over time;
Accessibility: Determines how other neural systems can interact with stored patterns;
Coherence Transfer: Describes how quantum correlations enable information transfer.
This mathematical structure explains how:
Neural activity creates persistent patterns in the vacuum field;
These patterns maintain quantum correlations despite environmental influences;
Information becomes distributed in a holographic-like manner;
Different neural systems can access the same field patterns independently.
🖲 4 - Information Theoretical Analysis
The holographic encoding of neural activity into the quantum vacuum field is modelled through an entangled state of the neural system and the vacuum field:
Where ∣n⟩neural represents the neural basis states, and ∣αn(t)⟩field denotes the corresponding coherent states of the vacuum field. The coefficients cn(t) capture the time-dependent superposition dynamics between neural states and their field-encoded counterparts. This entangled state means that the neural and field states are not independent but are correlated due to their interaction.
The second-order correlation function G(2)(x,x′,t) quantifies the spatial coherence of the field with a two-point correlation function, reflecting the correlation between field amplitudes at different points:
Where fk(x) are the mode functions, and ⟨bk†bk′⟩ quantifies mode occupations and coherence, capturing the spatial and temporal structure of the perturbations caused by neural states via creation and annihilation operators. This function replaces the classical notion of a holographic interference pattern with a fully quantum mechanical description of field correlations. This formulation also implies that the information is distributed, even for cases where the field is not in a thermal state and there are correlations between different modes, really interesting given the stochastic nature of the interaction.
The information capacity density ρinfo(x,t) is derived using the Von Neumann entropy of the field density matrix ρfield(x,t), quantifying the information encoded in the field:
Where ρ̂field(x,t) is the reduced density matrix of the field at position x and time t, and λₖ(x,t) are its eigenvalues. This provides a rigorous quantification of the information encoded in the field’s quantum state based on its probability distribution.
Finally, the degree of entanglement between the neural system and the vacuum field is quantified using the entanglement entropy Sent(t):
Where ρred(t) is the reduced density matrix of the neural system obtained by tracing out the field degrees of freedom from the total state ∣Ψ(t)⟩. This quantifies the non-classical correlations between the neural and field states, providing a measure of how much information is shared between the two systems due to their quantum entanglement.
It is worth mentioning that the classical concept of a holographic interference pattern I(r) is not directly applicable in this quantum framework, given that both encoding and potential retrieval of information are encoded within the correlations of the quantum field, described by G⁽²⁾(x,x',t), and the entanglement between the neural and field states, quantified by Sent(t). The interplay of neural perturbations and vacuum modes, captured by these quantum measures, replaces the classical notion of interference and provides a more accurate depiction of quantum information transfer.
🖲 5 - Attenuating Interaction Weakness
A weak interaction (Hint) implies weak perturbations of the quantum vacuum field. Given the background fluctuations of the ZPF and the noisy environment of the brain, these small perturbations are likely to be masked, be washed out or lose coherence (however, recent findings suggest robust coherence in biological systems, even in the brain, which may call for more careful decoherence claims). To address this issue, the hypothesis explores several mechanisms that could attenuate the effects of this interaction weakness. While external factors such as human-made EM fields, Schumann resonance, geomagnetic effects, and the broader “cosmic fluid” could contribute to both selective amplification (acting as cross-frequency “carrier waves”) and background noise, the following mechanisms focus on inherent dynamics within the proposed brain-ZPF interaction.
Nonlinear amplification effects can be introduced to capture potential emergent phenomena, such as amplification thresholds or bistability. This is modeled by the following equation:
Here, A represents an amplification factor, f(A) describes the nonlinear dynamics, D∇²A accounts for spatial diffusion of the amplification, and η(t) models stochastic fluctuations. The nonlinear term f(A) includes a linear growth term (μA), a saturation term (-βA³), and a sinusoidal term (γ sin(ωt)) that may represent external driving forces or oscillations.
Signal propagation within the ZPF is modeled using a Green’s function, a standard technique for describing propagation and diffusion of signals over space and time:
Here, S(x,t) represents the propagated signal, G(x-x', t-t') is the Green's function, A(x',t') is the amplification factor at position x' and time t', and ψ(x',t') represents the neural state at position x' and time t'.
Lastly, to address the issue of decoherence, a coherence protection mechanism is introduced to model quantum Zeno-like effects, where frequent “measurements” or interactions can inhibit decoherence:
Here, ρ is the density matrix of the system, H is the Hamiltonian, Ldiss represents dissipative processes, and Lprot is the coherence protection term. The Lindblad operators Lj and the rates Γj would need to be specified based on the specific physical mechanisms involved.
All these mechanisms, and potentially other synergistic effects are supposed to influence decoherence. However, a full and accurate model of complex interactions requires further investigation and advanced computational modeling, beyond the scope of this introduction.
🖲 6- Neural Network Dynamics
The dynamics of neural activity are modeled at a mesoscopic level, considering wave-like excitations within dendritic networks. The dendritic wave function (ψd) is described by a nonlinear Schrödinger equation:
Here, the term -(ħ²/2m)∇² represents the kinetic energy of the wave function ψd, interpreted as a quantum mechanical description of spatially distributed neural excitation. ψd can be understood as representing pre-oscillations or collective modes within the dendritic network. V(r) represents the potential energy landscape within the neural network, which could include contributions from synaptic coupling or the overall electrical potential. The parameter α is a coupling constant that determines the strength of the nonlinearity. This nonlinearity can account for complex interactions within the dendritic network, such as self-interactions or interactions between different dendritic branches.
The coupling between the neural network and the quantum field is described by the following equation for the evolution of the neural density matrix (ρneural):
Where −∇⋅J represents the continuity equation for the neural density, and J is the current density of neural excitation, describing the transport of neural activity within the network. The coupling term (iγ/ħ)[Φ(x,t), ρneural] describes the interaction between the quantum field (Φ(x,t)) and the neural density matrix (ρneural) through a commutator, consistent within the quantum mechanical framework. Finally, the term Lneural ρneural is a Lindblad term that accounts for dissipation and decoherence processes within the neural network itself, depicting interactions with surrounding biological environments.
🖲 7 - Process Equation
The evolution of the coupled neural-field system is described by a master equation that captures the full dynamics of information encoding, storage, and retrieval. This equation extends beyond simple unitary evolution to include the complex interplay between neural states and vacuum field perturbations, incorporating non-unitary dynamics due to interactions with the environment:
The equation decomposes the total dynamics into distinct but interrelated processes:
The first term, -i[Ĥ,ρtotal]/ħ, represents the coherent evolution under the total Hamiltonian, maintaining consistency with the fundamental interaction framework. This unitary evolution provides the baseline dynamics for information exchange between neural and field systems.
The capture superoperator Lcapture[ρtotal, A(ρ,t)] describes how neural coherence patterns become encoded in the vacuum field. It employs the same density functionals Fn(ρ) used in the interaction Hamiltonian for consistent treatment of neural-field coupling. The time-dependent coupling strength γc(t) modulates the capture efficiency based on neural system conditions.
The field evolution term Lfield[ρtotal, Φ(x,t)] governs how encoded information patterns evolve within the quantum vacuum. Using a non-local kernel K(x,t), it captures how field perturbations spread and interact across space and time, crucial for the holographic-like storage of information. The double commutator structure ensures proper quantum mechanical evolution of field states while preserving fundamental physical constraints.
The decoding superoperator Ldecode[ρtotal, Fn(ρ)] models how receiving neural systems interact with stored field patterns. Its parallel structure to the capture term, but with distinct coefficients βn(t), reflects the symmetry yet independence of encoding and retrieval processes. The time-dependent coupling γd(t) accounts for varying reception conditions.
Finally, the dissipation term Ldiss[ρtotal] uses the Lindblad form to incorporate realistic decoherence and energy dissipation effects. The time-dependent rates Γj(t) and multiple decay channels through operators Lj provide a sophisticated treatment of how biological conditions should affect quantum coherence.
Lastly, the probability of successful information transfer (𝑃transfer) between neural systems through the quantum vacuum field is given by a more sophisticated expression that accounts for multiple factors affecting transmission fidelity:
The probability 𝑃transfer is formulated as the trace of a success measurement operator M̂success(t) acting on the total system state, providing a proper quantum mechanical treatment of measurement outcomes. This operator formalism ensures that only physically meaningful transfer events are then counted.
The expression incorporates three key multiplicative factors:
First, the quantum mechanical transition amplitude |⟨ψreceiver|e-iĤt/ħ|ψsender⟩|² represents the basic probability of state transfer under ideal conditions. This term captures the fundamental quantum mechanical aspect of information transfer through the vacuum field.
Second, an exponential decay factor involving the time-integrated fidelity F[ρsender(t'), ρreceiver(t')] accounts for how well the sender and receiver states remain compatible throughout the transfer process. The time-dependent rate γ(t') modulates this decay based on environmental conditions.
Third, the field coherence functional C[Φ(x,t)] evaluates how well the vacuum field maintains the encoded information patterns. This term connects directly to the vacuum field perturbation patterns described earlier and accounts for field stability effects.
The overall efficiency factor η(t) encompasses various environmental and systematic effects that might influence transfer success. This time-dependent factor allows for realistic modeling of biological and environmental variations.
Challenges and Considerations
1. Testability- The FMHR mechanism faces significant challenges, primarily due to the subtle nature of the proposed interactions. Information is postulated to be encoded in the quantum field perturbation patterns, potentially via biophotonic emission patterns and Fourier transform processes in dendritic networks, projecting holographic interferences. However, quantum interactions in biological systems can be easily masked by thermal noise and background electromagnetic radiation. This inherent noise makes the detection of quantum effects in the brain complex, potentially demanding novel detection methods such as biophoton detectors or quantum coherence monitors. Similarly, the effects of quantum vacuum fluctuations are incredibly tiny, often far below the threshold of current experimental equipment. While we can observe the Casimir effect and vacuum fluctuations in certain conditions, capturing and isolating brain-induced fluctuations would be extraordinarily difficult, though not theoretically impossible.
2. While FMHR could potentially contribute to consciousness research by providing mechanisms for information integration and transfer, its primary framework is about quantum-mediated neural information dynamics, not consciousness itself. Unlike field theories of consciousness (like the electromagnetic field theory of McFadden or other quantum theories of consciousness), FMHR doesn’t:
Try to explain subjective experience;
Address the hard problem of consciousness;
Make claims about how conscious awareness emerges;
Position the field as the seat or substrate of consciousness;
This distinction is important because although FMHR does have “field” in its name, it is not a Field Theory of Consciousness, being instead more aligned with the concepts of Information Theory, quantum biology mechanisms, neural communication frameworks and holographic encoding principles.
3. Comparison with Henry Stapp’s Work: Henry Stapp work is centered around consciousness itself, while FMHR describes dynamics that interact with brain activity, which it claims to may or may not involve conscious thought. In his 1999 paper “Attention, Intention, and Will in Quantum Physics”, Stapp writes: “… the reduction is in that part of the state of the universe that constitutes the state of the body/brain of the person to whom the experience belongs: the reduction actualizes the pattern of activity that is sometimes called the ‘neural correlate’ of that conscious experience”, understood as if “each conscious experience, has as its physical counterpart a quantum state reduction” which renders Stapp’s neural correlate as a “pattern of activity may encode an intention and, thus, represent a ‘template for action’. An intentional decision for an action, preceding the action itself”. Here, Stapp’s theory explicitly incorporates circularity, where consciousness (macro-level) interacts with quantum processes (quantum-level), forming a feedback loop that ties subjective experience to physical reality. Conceptually, FMHR’s “proto-thought” does not imply circularity; instead, it suggests a precursor potential. Similarities aside, if we ignore Stapp’s feedback loop properties—where consciousness as a macro-level phenomenon drives a reduction at the quantum level, which then shapes the neural correlate—it seems Stapp “neural correlate” primarily describes a downwards causal event, while FMHR “proto-thought” describes an upwards potential. Together, both concepts then depict a bidirectional interaction between quantum processes and macro-level phenomena, a dynamic that can be illustrated with a simple rubric:
4. For the purposes of this introductory article, the ZPF is primarily conceptualized here as referring to the QED vacuum. However, a hybrid interpretation incorporating both QED and QCD vacua may offer a broader ontological perspective, contingent upon further scrutiny of the proposed mechanisms. As currently formulated, FMHR maintains an abstract compatibility with both vacua, allowing for a flexible interpretation of zero-point energy (ZPE) and the proposed dynamics of “proto-thoughts”, but the scale mismatch inherent to QCD processes and proposed biological interactions is in itself a conumdrum beyond the scope of this article.
5. “Quantum-brain” connections are often colored with common skepticism, and many professionals are certainly right to be quick in invoking cynicism, mainly due to the challenges of quantum-to-macro transitions and lack of biosignatures that would suggest quantum dynamics in organic systems, or specifically, in the central nervous system (CNS) as a whole (the brain and the spinal cord). As a personal anecdote, 99% of the time I find myself sneering at the simple mention of the word “quantum” too, and mind you: I have about twenty-two years of experience in the ICT industry, with the past six years alone working exclusively with neural networks and AI. So I get it, anything “real world quantum” is rare. However, this article excels in three key areas that make me confident it can be a good contribution to quantum conversations: A) It avoids common pitfalls of quantum consciousness theories; B) It introduces a novel perspective to information transfer with an original perspective on a multidisciplinary approach; and C) It provides detailed mathematical formalism, drawing on established quantum mechanics and field theory, going beyond speculative or unsubstantiated philosophical discourse. Finally, FMHR equations for its suggested mechanism do attempt to address two of the most common challenges regarding quantum biology:
The decoherence problem: common to popular narratives, biological systems and more specifically the brain’s “wetware”, are said to be “warm, humid, and noisy”, then taken as being unfavorable for quantum phenomena. FHMR addresses this issue from numerous perspectives outlined in the article, and while it assumes sustained coherence to be inherent to continuous neural activity and suggests that certain coherence protection mechanisms (akin to quantum Zeno effects) could reduce decoherence through frequent “measurements”, it also includes temperature and time-dependent modulation terms (γi(t,T) wihin its neural Hamiltonian to account for effects of physiological conditions and thermal fluctuations. FMHR also incorporates stochastic Schrödinger-like equations to model the interplay between deterministic quantum evolution and environmental noise; Finally, recent studies have suggested that coherence may be more stable than previously believed: refA, refB;
The scalability problem: how quantum-level phenomena can influence meso or even macroscopic processes is a subject of hot debate within both classical and quantum physics circles. FMHR employs a Hamiltonian framework that incorporates both neural oscillator terms and vacuum field interaction terms, and the equations explicitly handle the coupling between scales. For example, the interaction Hamiltonian (Hint) dynamically couples neural coherence states (âi†,âi) with quantum vacuum field modes (bk†,bk), enabling quantum-level perturbations to influence larger-scale neural dynamics; But as FMHR formulations are highly simplified at this point, we have room for more explicit representations. One readily available regards the integration of quantum coherence in ion channels as a localized mechanism that complements dentritic oscillations, here represented by extending the neural density matrix equation to include ion channel states:
\(\begin{gather*} \large \frac{\partial}{\partial t} \left( \rho_{\text{neural}} \otimes \rho_{\text{ion}} \right) = -i \left[ \hat{H}, \rho_{\text{neural}} \otimes \rho_{\text{ion}} \right] + \mathcal{L}_{\text{neural}}[\rho_{\text{neural}}] + \\\large\mathcal{L}_{\text{ion}}[\rho_{\text{ion}}] + \mathcal{L}_{\text{coupling}}[\rho_{\text{neural}} \otimes \rho_{\text{ion}}]\\ \newline \text{Where:}\\ \rho_{\text{neural}} \space \small\text{= Density matrix representing the state of the neural network.}\\ \rho_{\text{ion}} \space \small\text{= Density matrix representing the state of the ion channels.}\\ \otimes \space \small\text{= Tensor product.}\\ \hat{H} = \hat{H}_{\text{neural}} + \hat{H}_{\text{ion}} + \hat{H}_{\text{int}} \space \small\text{= The total Hamiltonian.}\\ \newline \end{gather*}\)Where the Lindblad terms can be expressed as:
\(\begin{gather*} \mathcal{L}_{\text{neural}}[\rho_{\text{neural}}] = \sum_{j} \Gamma_{j} \left( 2 L_{j} \rho_{\text{neural}} L_{j}^{\dagger} - L_{j}^{\dagger} L_{j} \rho_{\text{neural}} - \rho_{\text{neural}} L_{j}^{\dagger} L_{j} \right)\\ \mathcal{L}_{\text{ion}}[\rho_{\text{ion}}] = \sum_{k} \gamma_{k} \left( 2 M_{k} \rho_{\text{ion}} M_{k}^{\dagger} - M_{k}^{\dagger} M_{k} \rho_{\text{ion}} - \rho_{\text{ion}} M_{k}^{\dagger} M_{k} \right) \\ \mathcal{L}_{\text{coupling}}[\rho_{\text{neural}} \otimes \rho_{\text{ion}}] = \sum_{l} \lambda_{l} \left( 2 N_{l} \left( \rho_{\text{neural}} \otimes \rho_{\text{ion}} \right) N_{l}^{\dagger} - N_{l}^{\dagger} N_{l} \left( \rho_{\text{neural}} \otimes \rho_{\text{ion}} \right) - \left( \rho_{\text{neural}} \otimes \rho_{\text{ion}} \right) N_{l}^{\dagger} N_{l} \right)\\ \end{gather*}\)Here the Lindblad superoperator for the neural network describes decoherence and dissipation processes. The Lj are jump operators representing specific transitions in the neural network, and the Γj are their corresponding rates. Moreover, the superoperator for ion channels accounts for their decoherence, the Mk are jump operators representing specific transitions in the ion channels, and the γk are their corresponding rates. And lastly, in the coupling superoperator the Nl are jump operators of coupled transitions and the λl cover their rates.
This integration not only addresses the scalability problem by providing a plausible pathway for quantum-level events to influence macroscopic neural activity but also demonstrates the modularity of the FMHR framework. Other biological or quantum subsystems can likely be similarly integrated using density matrix representations, making the FMHR model more versatile and testable.
6. Perhaps because of its name, the vast majority of people believe brain activity to be about activation processes, assuming cognitive functions to be about activation and deactivation of regions, without understanding inhibition to be an active process, rather than just the absence of excitation. Neurons are primarily responsible for excitatory signaling, while glial cells, such as astrocytes, play a vital role in inhibition and neuromodulation. Such balance of excitation and inhibition, critical from individual synapses to large-scale networks, is what brain activity really stands for. But importantly, states of inhibition can be signals of functional brain activity, or in other words, numerous types of processes in the brain can be modulated not by activity, but by inhibitory potentials, and unlike neurons, glial cells do not produce electrical impulse, making it harder for us to detect inhibition-based processes. In a similar fashion, just as many people misunderstand the role of inhibition, so too is there a common misconception about brain energy consumption. Studies have shown that the brain’s energy consumption is primarily proportional to the total volume of neurons, not the number of synapses or cognitive abilities, which is another way to say that complex cerebral activities in humans are not associated with significantly more energy demand than at rest. Both these facts about brains raise an important question: if there are no substantial change in energy consumption for most tasks performed by the brain, and some specific function may in fact be not the reflection of an activity, but of an inhibition instead, could this explain why FMHR biomarkers traces were always missed? As it stands, it seems obvious that we may need better methods to detect metabolic fluctuations, significant states of inhibition, and afferent (incoming) and efferent (outgoing) neuromodulation, as without these, we may never find a mechanism akin or similar to the one described by the FMHR. This relates to a broader issue in neuroscience: our ability to discover new mechanisms is limited by the assumptions built into our current detection technologies and their calibration.
7. The no-cloning theorem states that it is impossible to create an independent, identical copy of an arbitrary unknown quantum state due to the linearity of quantum mechanics. FMHR avoids this conflict because it does not propose cloning quantum states, proposing instead a mechanism that collects probabilistic features of quantum coherence states—akin to a 4D version of a “3D pinscreen toy”. Theoretically, such capture is closer to a ZPF interpretation of the brain state, not as a computational representation, but as a snapshot of the interplay between quantum fluctuations and the brain operational state. The FMHR aligns more with theories of the brain as a complex, adaptive system: It sees cognitive processes as emergent properties of dynamic interactions across multiple scales—quantum, micro, mesoscopic, and macroscopic—rather than deterministic operations on discrete data. Data in the ZPF emphasizes holographic and distributed encoding, reflecting biological realities rather than qubits. ZPF imprints are partial and contextual “snapshots” of ongoing CNS processes, not exact replicas. Finally, the ZPF isn’t a medium in the traditional sense, but it holds a stochastic chance to act as one many times throughout the day.
Discussion
The present hypothesis offers a novel perspective on a potential interplay between neural activity and the quantum vacuum field, exploring the possibility of subtle, autonomous, and probabilistic interactions that could encode and transmit information reflected in neural quantum coherence states as a natural phenomenon, occurring at the intersection of quantum mechanics and biological systems.
I have written this particular article/hypothesis in a single week, which often translates into errors of all kinds and flavors. While I think I am very likely to be pushing the boundaries of scientific rigor, I consider the FMHR to be a cool tangent about the interplay of quantum mechanics and the universe that surrounds us, challenging Quantum Mind theorizations without trying to explain what happens in brains from a “human locked” frame of reference. To be blunt, the process described by the FMHR would account for any brain, and while I do not believe this would mean interspecies interactions, I think it is cool that all life may express itself not only as coexisting entities, but also as part of a wave of information about information. All in all, I had to write this series to put my mind into words, without fear of being wrong, in the hopes that eventually, I can hone it into something better. Additionally, I also believe the process described here to be both planet and time bounded, meaning captured information is very likely to not survive for longer periods, which probably also does not allow this information to persist much further in space.
While I am not claiming to corroborate concepts such as a noosphere, the proposed dynamics suggest a possible physical mechanism that could contribute to a more interconnected view of reality. Specifically, if we consider the quantum vacuum as part of a broader “cosmic fluid” it is perhaps even more conceivable that alternative or compounded mechanisms for amplification or mediation of the proposed brain-ZPF interaction could exist, further enhancing the potential for subtle quantum effects to somehow affect or have a role in macroscopic events. This broader context could offer partial explanations for several observed social/macrosocial phenomena, including:
Collective Emotions and Social Contagion: If a strong emotional state in one individual generates a significant ZPF perturbation, under specific conditions it might influence the neural activity of others, potentially contributing to the spread of emotions within a population;
Social Learning and Mimesis: If observing a behavior leads to a specific neural state that perturbs the ZPF, others observing the same behavior could be more likely to adopt similar neural states and thus learn the behavior more readily;
Emergence of Similar Cultural Patterns: The hypothesis questions if characteristic ZPF perturbations associated with certain mental processes could contribute to the independent emergence of similar ideas or cultural practices in different populations.
In providing a mechanistic framework for exploring potential connections between quantum mechanics, neuroscience, and collective behavior, this work aims to stimulate further research and encourage a more open exploration of non-local quantum dynamics in biological systems. It suggests that reality may possess a deeper level of interconnectedness than currently understood, and this is certainly more than we had yesterday.
FMHR Disclaimer
As it is, this hypothesis remains speculative and requires further theoretical development and rigorous experimental investigation. Moreover, while grounded in established principles, the proposed interactions are difficult to be objectively tested and may require multidisciplinary efforts to be validated. Highly speculative connections and metaphysical interpretations such as anomalous cognition (AC) and anomalous information reception (AIR) are not encouraged.




